sucesiones
sucesiones
Una sucesión es un conjunto de cosas (normalmente números) una detrás de otra, en un cierto orden.
las sucesiones pueden ser finitas o infinitas también llamadas geométrica y aritmética
Son aritméticas cuando cada término es la suma del término anterior más un número constante, al que llamamos diferencia y denotamos por d. Es decir,
Son geométricas cuando cada término es el término anterior multiplicado por un número constante, al que llamamos razón y denotamos por r . Es decir,
an+1=an⋅r
Fórmulas
| SUCESIÓN ARITMÉTICA | |
|---|---|
Es de la forma
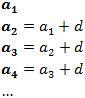 | |
Diferencia
|
Término general
|
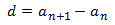 | 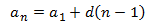 |
Suma de los n primeros términos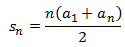 | |
| SUCESIÓN GEOMÉTRICA | |
Es de la forma
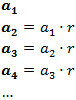 | |
Razón
|
Término general
|
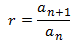 | 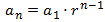 |
Suma de los n primeros términos
|
Suma de todos los términos
|
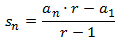 | 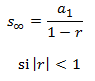 |
Una sucesión aritmética es decreciente si d < 0, creciente si d > 0 y constante si d = 0.
Una sucesión geométrica cuyo primer término es positivo es decreciente si y creciente si . Si el primer término es negativo, es creciente si y decrecientesi . Independientemente del primer término, es constante si y es alternada si es negativo (cambia el signo en cada término).
ejemplos
Los números son
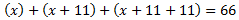
Es decir, tenemos una ecuación de primer grado:

Luego los números son 11, 22, 33.
La ecuación la podemos expresar en términos de una progresión como
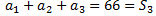
es decir, como la suma de los tres primeros términos de una progresión cuyo término general es
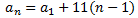
Demostrar que en cualquier sucesión geométrica positiva, cada término es la raíz cuadrada del producto de su término anterior por su término siguiente. Es decir,
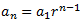
y queremos demostrar que
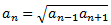
Para demostrarlo, calculamos y usando el término general:
y sustituimos en el radicando. Quedará demostrado al obtener que dicha raíz es justamente el término :
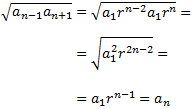


Comentarios
Publicar un comentario